Table of Contents
Mimicking Molecules: Pickering Particles and Catalytic Colloidal Conversion
Do not disturb my rings!
Colloids have a rich history of being used as big atoms mimicking real atoms to study crystallization, gelation and the glass transition of condensed matter. Emulating the dynamics of molecules, however, has remained elusive. Recent advances in colloid chemistry allow patchy particles to be synthesized with accurate control over shape, functionality and coordination number. In this chapter, I discuss how colloidal alkanes, specifically colloidal cyclopentane, assembled from tetrameric patchy particles by critical Casimir forces undergo the same chemical transformations as their atomic counterparts, allowing their dynamics to be studied in real time. Transitions between chair and twist conformations in colloidal cyclopentane are observed directly, and we elucidate the interplay of bond bending strain and entropy in the molecular transition states and ring-opening reactions. These results open the door to investigate complex molecular kinetics and molecular reactions in the high-temperature classical limit, in which the colloidal analogue becomes a good model.
1. Introduction
Colloidal particles have been much used to study phase transitions such as crystallization, gelation and the glass transition of condensed matter at experimentally accessible length and time scales1). In this analogy, atoms are represented by homogeneous colloidal spheres with tunable interactions between them. This approach has been successful, and many of the lessons learnt are directly applicable to fields such as photonics 2), opto-electronics 3), and bio-materials 4).
Compared to these crystalline systems, molecules typically have a much richer structure: atoms are generally bonded directionally into molecules via valence. For example, in aliphatic organic compounds in which a carbon atom has four bonds, such as methane (\(\)), the carbon atom is in an \(sp^3\) hybridized state, binding ligands in a tetrahedral arrangement at approx. 109.5°C bond angles. However, although many theoretical and simulation studies exist, achieving directional bonding in colloidal systems is challenging, and reliable experimental systems are scarce 5)6)7). Recently developed patchy particles, decorated with patches of specific surface chemistry, with well-defined symmetry, allow reproducing the geometry of valence bonds8)9)10)11)12)13). While these particles mimic the rigid shape of small molecules, emulating molecular reactions and conformational dynamics would require degrees of freedom similar to that of organic molecules, through reversible, specific patch-patch interactions, tunable on the scale of \(k_T\), the thermal energy14). Such interactions would open the door to colloidal molecular chemistry: molecules that consist of colloidal particles instead of atoms, reacting at the nano and micrometer scale, directly observable by microscopy. This in turn could unlock design paths for nanostructured materials15).
Specific, adjustable colloidal interactions arise in binary solvents close to their critical point. This critical Casimir force results from the confinement of solvent fluctuations between particle surfaces in a near-critical mixture, giving rise to an effective interaction that is precisely tunable with temperature and the adsorption preferences of the confining surfaces, see chapter 2. For isotropic particles, these interactions have provided insight into gas-liquid and liquid-solid phase transitions16)17) as well as gelation 18). Combined with patchy particles exhibiting surface patches of specific solvent affinity, the interactions become directed, and may allow the reversible assembly of more complex, molecule-like structures, and their direct particle-scale observation.
In this chapter, we show that patchy particles bonded via critical Casimir forces allow direct-space investigation of molecular dynamics, providing insight into thermally activated molecular transition states. We bind dimer and tetramer particles into colloidal alkanes, resembling alkane molecules, such as colloidal (cyclo)butane, butyne, cyclopentane, and cyclohexane, and investigate their dynamics directly in real space using confocal microscopy. We find that just as molecular cyclopentane, colloidal cyclopentane exhibits envelope and twist conformations that interconvert in time, and we follow the kinetic pathway in great detail. Furthermore, we measure the free energy and corresponding bending energy directly from the observed molecular trajectory; this allows us to elucidate the interplay of bond strain and entropy in thermal and catalytic dissociation reactions of colloidal cyclopentane. These results open up directions for studying the dynamics of molecules using precisely coordinated patchy particles, and for building complex nano- and micrometer-scale materials 19).
2. Results
2.1. Colloid Fabrication
We use patchy particles described in chapter 2, particle batch A&B from Table 1. To quickly recap: patchy particles are polystyrene (PS) and 3-(trimethoxysilyl)propyl methacrylate (TPM) spheres produced by colloidal fusion 20). The synthesis yields particles with precisely linearly and tetrahedrally coordinated, fluorescently labelled TPM patches in a PS matrix (Figure 1a). The tetrapatch particles have a diameter of $(\sigma_\mathrm{tetra} = $ 3.7μm, dipatch particles $\sigma_\mathrm{di} = $3.2μm and both have a patch diameter 0.5μm $> d_\mathrm{p} >$ 0.4μm; sufficiently small to allow only a single other patch to bind. Di- and tetrapatch particles with number ratio 1:3 are dispersed at a volume fraction of \(\phi= 0.01\) in a binary mixture of lutidine and water close to its critical point. We also add 1mM $\mathrm{MgSO_4}$ to screen the electrostatic repulsion and enhance the lutidine adsorption of the patches, see chapter 2. Upon approaching the solvent demixing temperature \(T_\mathrm{cx} = \)33.8°C, lutidine-rich fluctuations arise between the patches, binding them into a covalent bond analogue by critical Casimir interactions as illustrated in Figure 1b. To assemble colloidal molecules, we heat the sample to \(Delta T = \)0.04K below \(T_\mathrm{cx}\), resulting in a predicted binding energy of the patches of approximately \(15k_\mathrm{B}T\) (see section 4.4) 21)22).
2.2. Colloidal Alkanes
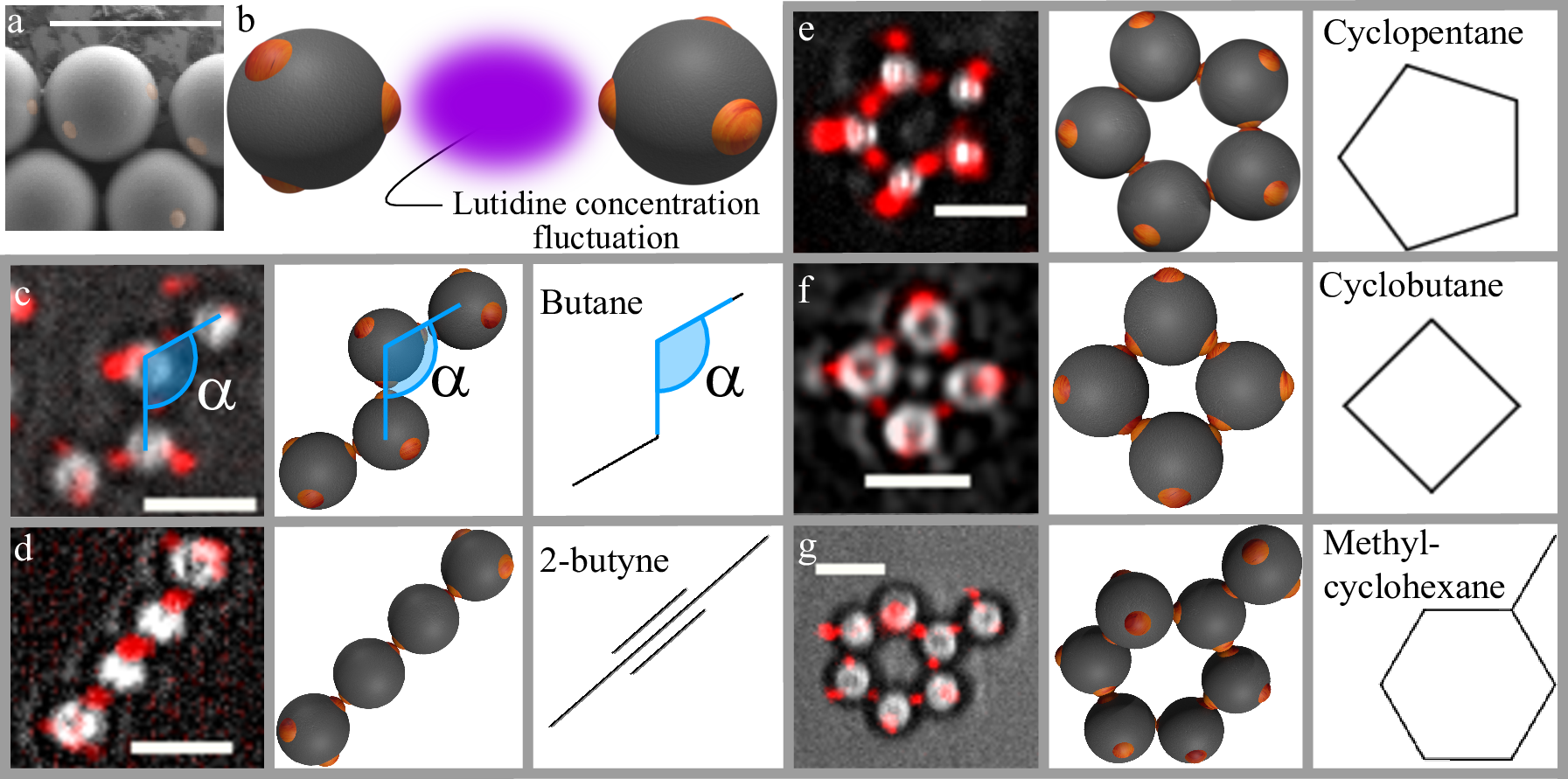
After a few hours, we observe bonded structures exhibiting the coordination and bond angles of carbon atoms in organic molecules, as shown in Figure 1c to g (see section 4.5 for assembly details). A zigzag chain of four tetrapatch particles exhibiting the carbon backbone structure of butane is shown in Figure 1d. A colloidal analogue of 2-butyne, consisting of 2 central dipatch particles with 2 tetrapatch particles capping both ends, is shown in Figure 1e. Analogues of cyclic alkanes, ubiquitous in carbon chemistry, are shown in Figure 1e-g. Rings consisting of four, five, and six tetrapatch particles are observed, which we identify as colloidal cyclobutane, cyclopentane and cyclohexane. We note that unlike their atomic counterpart, these colloidal molecules have unsaturated patches, lacking their ‘hydrogen atoms’, which may lead to some difference in their reactivity and conformations.
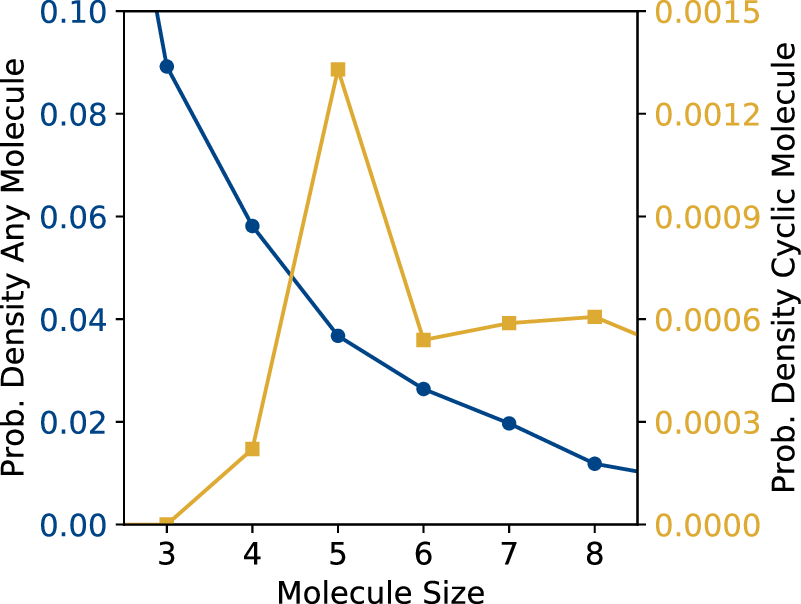
We show size distributions of colloidal molecules in Figure 2. Clearly, smaller structures are in the majority, but a significant population of larger structures is present in the sample. The population decreases exponentially with size, as predicted for patchy particle systems23). Cyclic molecules, however, show a clear preference for a certain number of particles, reflecting their compatibility with the tetrahedral bond angle. Colloidal cyclobutane (Figure 1f) is rarely encountered in our samples. This is not surprising considering its highly strained bond angles. In this configuration, two bonded neighbours make an angle of 90°, far from the ideal angle of 109.5°, causing high bond strain. For atomic cyclobutane, this high bond strain is known to cause the enhanced reactivity of cyclobutane compared to butane, making it much less stable than cyclopentane and cyclohexane that exhibit bond angles much closer to 109.5°. Indeed, we find that colloidal cyclopentane (Figure 1e is much more ubiquitous in the sample, and by far the most observed colloidal ring structure. Its bonds are much closer to the ideal 109.5° tetrahedral bond angle, compared to cyclobutane. Curiously, six-membered rings - cyclohexanes - are much less frequently observed, even though they have a lower bond angle strain, probably due to kinetic effects 24).
2.3. Conformations of Colloidal Cyclopentane
We focus on the most frequently observed cyclic structure, colloidal cyclopentane, and image its three-dimensional bonding arrangement using confocal microscopy. The three-dimensional reconstructions reveal three basic conformations (Figure 3a): a planar conformation with all particles in the same plane, an ‘envelope’ conformation, with one particle sticking out, and a ‘twist’ conformation with one particle sticking out above, and an adjacent particle sticking out below the plane. Just as its colloidal counterpart, atomic cyclopentane also shows these conformations; like most cyclic molecules, the internal angles of the ring are not compatible with the 109.5° bonding angle of the tetrahedral symmetry. In planar cyclopentane, the angles are only slightly lower, at 108°; nevertheless, due to energetic considerations - the steric hindrance of hydrogen atoms and torsional strain - atomic cyclopentane is virtually always puckered out of plane25).
Conversely, colloidal cyclobutane shows virtually no puckering, as shown by the significantly narrower bond angle distributions in Figure 3b. Cyclobutane shows a much narrower bond angle distribution, in particular lacking the tail towards larger angles as observed for cyclopentane, which is a signature of its puckering configurations (see section 4.6 for a comparison of bond angle distributions of different colloidal molecules). Hence, while there is a driving force for out of plane movement of cyclopentane, and thus a relatively wide angular distribution, cyclobutane bonds are stiffer, forcing the highly strained ring into a narrowly confined configuration (video available online 26)).
2.4. Pseudorotation
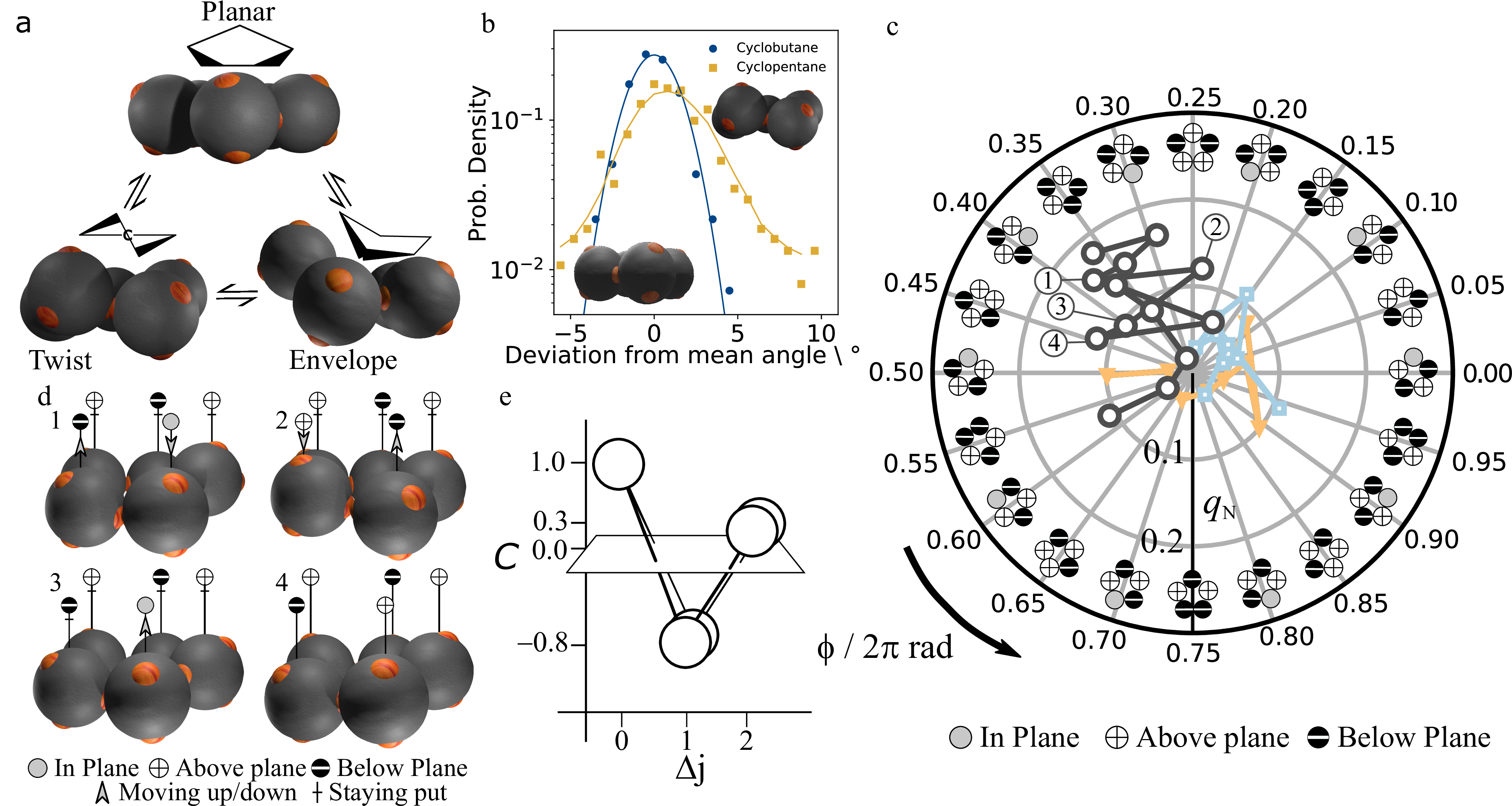
For each particle in cyclopentane, there are two envelope and two twist conformations, as shown in Figure 3c. In molecular cyclopentane, these conformations are thought to interconvert continuously. This process is known as pseudo-rotation, and has been suggested as early as the 40s, but so far has only been confirmed by indirect spectroscopic evidence 27)28). Likewise, we find that in colloidal cyclopentane, envelope and twist conformations interconvert continuously. To follow the pseudorotation directly in real space, we rapidly acquire image stacks every twelve seconds, roughly 2 times faster than the typical relaxation time of a configuration, see section 4.7. Three-dimensional reconstructions reveal the pseudorotation of colloidal cyclopentane in Figure 3d and online videos29)30). From frame 1 to 2, a particle (left) flips from below to above the plane, while its in-plane neighbour moves down out of plane. From frame 3 to 4 a characteristic change from envelope to a neighbouring twist conformation occurs, corresponding to the upward motion of the (central) in-plane particle. Remarkably, during these transition states, the ring always remains highly puckered. To show this, we correlate the vertical displacements, \(z_i\), of nearest and second-nearest neighbour particles and find that they are strongly anticorrelated, as shown in Figure 3e: the upward movement of a particle typically results in the downward movement of the neighbouring particle, followed by an upward movement of the next nearest neighbour. These correlations highlight the strongly correlated nature of the pseudorotation of colloidal cyclopentane, and suggest that interesting collective behaviour is to be expected in larger colloidal molecules.
To analyse the pseudorotation in detail, we determine the puckering amplitude \(q\) and phase \(\phi\) from the out-of-plane displacements \(z_i\) of the particles. Together, \(q\) and \(\phi\) form a polar phase space describing all possible puckering conformations. Given an average plane through the ring, \(q\) is a measure of the resulting amplitude of the out-of-plane displacements, while \(\phi\) tells us in what conformation the ring is, as indicated schematically in Figure 3c 31) (see section 4.3 for formal definition of \(q\) and \(\phi\)). A polar plot of the pseudorotation trajectory in \((q,\phi)\) space is shown in Figure 3c (see online videos for animations 32)33)). The coordinated up and down motion leads to pronounced changes in the puckering phase (phase change from frame 1 to 2 to 3 to 4). For example, the large phase change from 2 to 3 corresponds to a change from twist to a next-nearest envelope conformation, while that from 3 to 4 corresponds to a transition from twist to envelope, as shown by comparison of the trace in Figure 3c with the corresponding 2D representations.
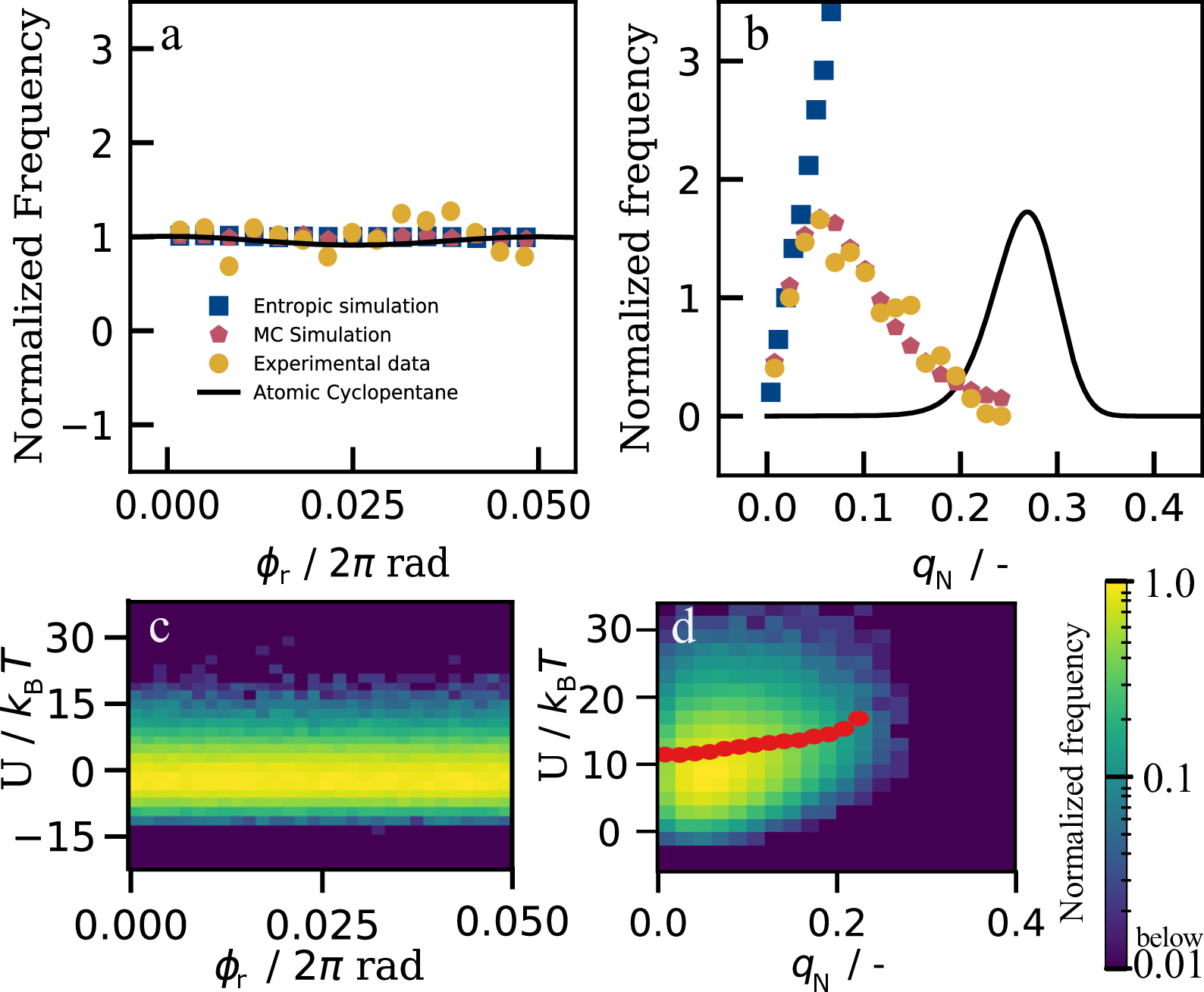
To explore the full statistics, we follow more rings, and determine distributions of the reduced puckering phase $\phi_\mathrm{r}$ and amplitude \(q\) as shown in Figure 4a&b. The reduced puckering phase indicates how far a particular configuration is between an envelope ($\phi_\mathrm{r} = 0$) and a twist ($\phi_\mathrm{r} = 0.05$) conformation. The flat distribution of $\phi_\mathrm{r}$ indicates that, just like in atomic cyclopentane, there is no preference for either envelope or twist conformation, nor any conformation in between. This is different for the puckering amplitude \(q\) (Figure 4b): Planar conformations with \(q \approx 0\) are almost never observed, while mildly puckered configurations with \(q \approx 0.15\) are most prevalent. As shown by simulations in section 4.4, the peak position depends on the presence of gravity: without gravity, the maximum of the probability density is shifted towards larger values (\(q_\mathrm{N} \approx 0.15\)) compared to the experimental measurement, meaning that the colloidal cyclopentane ring is more puckered in a system without gravity, as expected. Nevertheless, the presence of a finite puckering amplitude is surprising from an energetic point of view, as the flat ring (\(q = 0\)) has both the lowest bending and gravitational energy.
However, the entropy of this state is also the lowest: there is only one way to place the particles into a flat ring; even a small amount of puckering will unlock many configurational microstates, thus increasing the entropy.
To estimate the entropic contribution, we consider a ring of five freely joint particles moving up and down independently. The corresponding probability distribution \(P(q)\) increases linearly with \(q\) (Figure 4b), reflecting the increasing number of configurations. The experimental distribution initially follows this trend, but then peaks and diminishes. We associate this decrease with the increasing bending energy cost \(U(q)\) suppressing high-puckering amplitude configurations.
Together, entropic and bending energy contributions give rise to the free energy $F(q) = U(q) - TS(q)$, where $S(q) = k_\mathrm{B} T \ln P(q)$ is the entropy associated with the ring configurations. In thermal equilibrium, puckering amplitudes follow a Boltzmann distribution $f(q) \propto \mathrm{exp}(-F(q)/k_\mathrm{B}T)$. We invert this relation to determine the average bending energy from the measured distribution $U(q) = k_\mathrm{B} T \ln \frac{P(q)}{f(q)} + U_0$, where \(U_0\) is an arbitrary reference energy, see section 4.8. The resultant \(U(q)\) indeed reveals an increasing bending energy with puckering amplitude, as shown in Figure 4d (red circles).
These trends are confirmed in Monte Carlo (MC) simulations of five tetrapatch particles interacting with effective critical Casimir potentials as detailed in section 4.4. Their puckering distributions are in excellent agreement with the experimental data, as shown in Figure 4. Furthermore, we compute the total bending energy \(U\) directly from the strained bonds for each observed configuration; the resulting probability contour plot shows good agreement with the experimental data (Figure 4d).
Interestingly, atomic cyclopentane shows a distribution peaked at much higher values of \(q\). Contrary to colloidal cyclopentane, the molecule experiences additional H-H steric repulsions as well as torsional strain, leading to a stronger degree of puckering. Nevertheless, the subsequent decline indicates occurrence of additional bending energy, similar to the colloidal analogue.
2.5. Ring Breaking and Catalytic Reactions
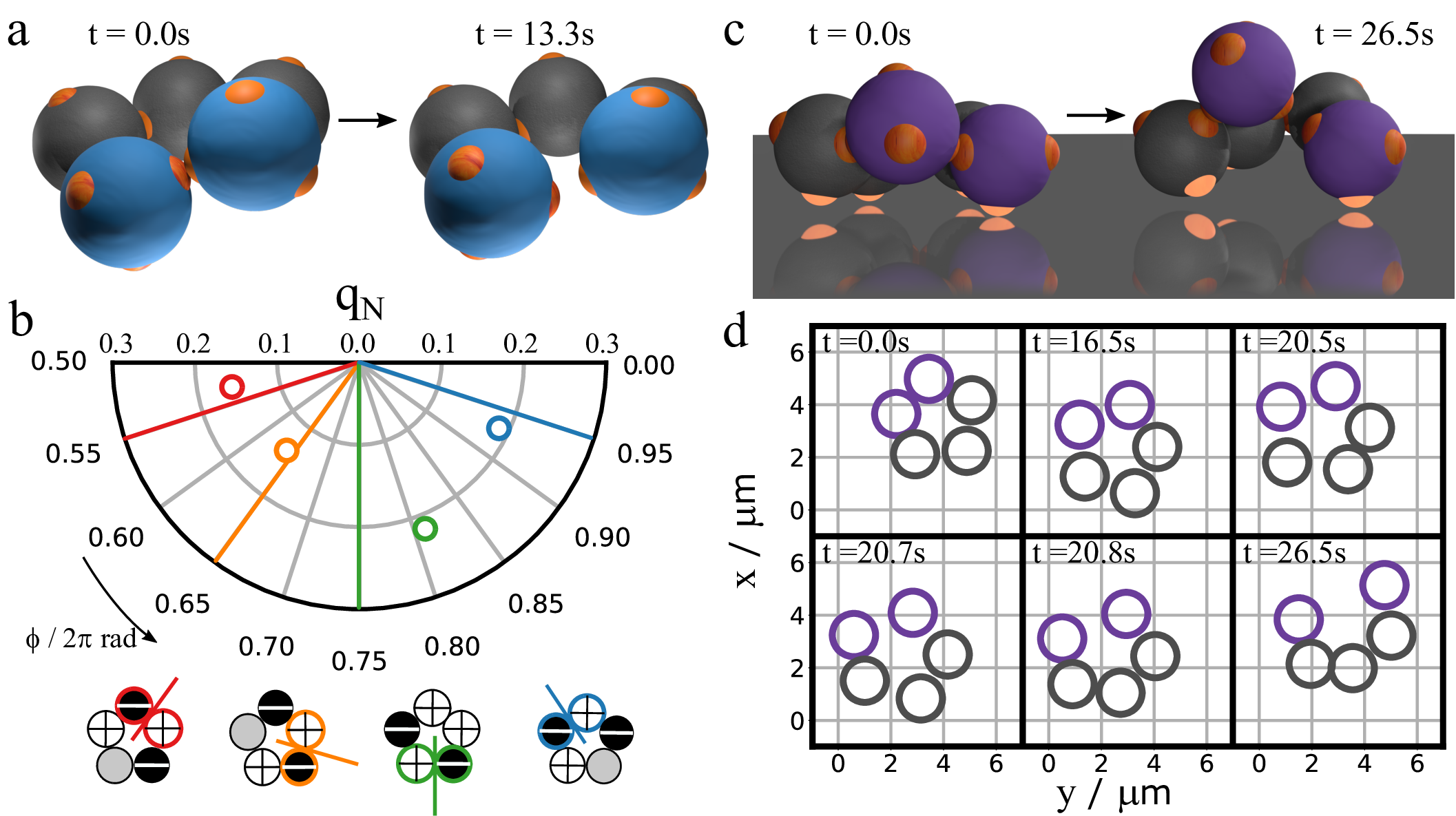
We fully exploit the direct observation of colloidal cyclopentane by studying ring-opening reactions. Rings occasionally break up as shown in Figure 5a and online video 34); this breakup is the thermal ring-opening reaction of colloidal cyclopentane to pentane (formally a pentane bi-radical). Interestingly, we find that just before breaking, rings always exhibit a high puckering amplitude, as shown in Figure 5b. Moreover, the bond breaking occurs at a particle strongly involved in the puckering, as shown by comparing the puckering phase just before bond breaking with the breaking point in Figure 5b. Because a high puckering amplitude corresponds to high bond strain, a large energy gain is made by breaking the bond. These results highlight the importance of bond-bending strain in the thermal dissociation of colloidal cyclopentane. Furthermore, the high \(q\) values just before breaking suggest that the reactivity of cyclopentane is highest for extreme puckering amplitudes, in the far high-\(q\) tail of the distribution in Figure 4b. We speculate that a similar mechanism may apply to atomic cyclopentane. Indeed, thermal ring-breaking reactions typically occur in cyclopentane and methyl-cyclopentane 35), which unlike higher-symmetry cyclic compounds like cyclohexane exhibit significant bond strain.
For atomic cyclopentane, a catalyst can greatly accelerate the ring opening reaction by offering attractive binding sites. For example, noble metal surfaces and mesoporous materials can achieve some selectivity in the ring opening reaction 36)37), but the mechanism is complex and poorly understood. To investigate such catalytic reactions in colloidal cyclopentane, we assemble rings in the bulk and sediment them onto a hydrophobic surface to which the particle patches bind. We find that this greatly speeds up the ring dissociation: a few minutes after surface adsorption, a ring breaks and opens, as shown in Fig 5c&d. Upon adsorption, 3 to 4 particle patches bind to the substrate (highlighted in Figure 5c), confining the ring to the surface, and effectively freezing it in a single envelope conformation. At the same time, the ring can still move laterally and diffuse along the substrate, before it opens (Figure 5d). The binding-induced angular strain, together with the entropically unfavourable locking of configurations, causes the ring to break easily. The hydrophobically treated substrate serving as a catalyst thus allows direct observation of the interplay of conformations, bond geometry and surface interaction in the catalytic dissociation process. This makes our colloidal model very suitable for the study of geometric effects of catalysts, in absence of any electronic or support effects, using designed colloidal crystal surfaces or templates with defined symmetry, lattice constant and domain size. Fast confocal microscopy imaging can then give detailed insight into energies along the reaction coordinate, identifying the transition states in these catalytic processes.
3. Discussion
The direct observation of pseudorotation and catalytic reactions of colloidal cyclopentane offers insight into transition states in a molecular dissociation reaction. As the thermal energy \(k_T\) is of the same order as the bond energy, the colloidal molecule corresponds to its high-temperature molecular counterpart. The ratio of 15 for the bond energy to \(k_T\) in our experiments would correspond to a temperature of \(640\)K for atomic cyclopentane, as can be estimated from its C-C bond energy of \(80\)kJ/mol. In this limit, the quantum mechanical energy spectrum of the low-frequency modes of the molecule becomes quasi-continuous, and classical behaviour is expected to emerge, suggesting that the colloidal analogue becomes a good model.
Our results highlight the importance of bond strain in the dissociation process, and suggest specific catalyst design that takes advantage of the puckering amplitude in the ring breaking process. These results pave the way to the investigation of molecular kinetics by detailed direct observation of colloidal analogues, elucidating transition states, kinetic pathways and correlations in molecular reactions 38). The exquisite temperature control afforded by the critical Casimir interaction creates opportunities for molecular and supramolecular colloidal design following equilibrium and non-equilibrium routes, and the investigation of dynamic assembly pathways. The demonstrated accurate binding control opens up pathways to colloidal molecular chemistry, in which bond-stretch and -bend potential-energy functions can be tuned by the experimentalist, and all the reactions, not only ring opening but also synthesis, homogeneous catalysis, and polymerization can be followed in real time using a conventional microscope to observe the reacting colloidal atoms.
4. Appendix
4.1. Sample Preparation and History
Particles are left to sediment to the bottom of the sample at room temperature before measurements. We choose a particle concentration such that the surface coverage is between \(\phi=0.10\) and \(\phi=0.15\) after sedimentation. We then start increasing temperature to switch on the critical Casimir attraction and assemble the structures.
In an experiment, we heat the sample to 0.04°C below the phase separation temperature of the lutidine-water mixture, inducing critical Casimir attraction between patches. The structures then grow by two-dimensional diffusion in the plane. No mixing is necessary. After several hours of equilibration, we investigate the structures using a 63x oil-immersion objective.
4.1.1. Catalytic Conversion
For the catalytic experiments, the samples are prepared in capillaries which have been made hydrophobic using the gas silanization reaction described in chapter 2. In the catalytic experiments, we use patchy particle batch C in Table 1 because those particles sediment slower and have a larger attractive temperature range between \(T_\mathrm{a}\) and \(T_\mathrm{cx}\) of approximately 0.20°C. Particles are left to sediment on one side of the capillaries. Then, we raise the temperature to \(\Delta T = 0.10\)°C and flip the sample over so the particles are in free fall. In this free fall, the particles assemble into (among other things) cyclopentane. When the ring is almost at the bottom of the sample, we lower the temperature to \(\Delta T = 0.17\) °C, and observe the adsorption of the ring to the surface and its subsequent breakup using a 100x oil-immersion objective.
4.2. Confocal Microscopy and Particle Tracking
We image the assembled structures using confocal microscope image stacks, alternating with bright field images. To follow a colloidal molecule in time, we acquire around 100 image stacks and bright field images during a time interval of 12 minutes. The particles and patch positions are then determined using the algorithms described in section 3.3. This yields an accurate 3D position vector \(\mathbf{R}_j\) of each particle \(j\) of a ring.
Finally, we use an algorithm which eliminates all rings which have unrealistically high or low angles between particles to further eliminate any data with particles placed on the wrong positions, which is confirmed by manual inspection of the video
4.3. Pseudorotation in Polar Coordinates
We use the method by Cremer and Pople39) to find the ring puckering coordinates for each particle configuration. This is done by expressing the positions \(_j\) of the particles in a new coordinate system. In this new coordinate system, the average plane through all particles forms the \(xy\)-plane, and the \(z\)-displacement \(z_j\) is the distance of a particle from this plane.
This new coordinate system must satisfy
$$ \sum^{5}_{j=1} \mathbf{R}_j = \mathbf{0} ~~\text{(origin set to centre of mass),} $$
meaning that the origin of the system is at the centre of mass of the five particles. We further enforce
$$\sum^{5}_{j=1} z_j = 0 ~~\text{(mean plane through origin),}$$
which means all \(z\)-displacement \(z_j\) in the new coordinate systems average out to zero: the mean plane must be the average of the particles. We choose the unit vector \(\) going through any of the five particles as a convenient \(x\)-axis. Unfortunately, these equations do not yet yield a unique average plane through the five particles: multiple planes can be drawn that will all satisfy the above conditions. Therefore, we further impose the conditions
$$ \sum^{5}_{j=1} z_j \cos[2\pi(j-1)/N] = 0$$
$$ \sum^{5}_{j=1} z_j \sin[2\pi(j-1)/N] = 0$$
which will fix the plane uniquely. In the case of a regular planar polygon, these relations correspond to the condition that a small displacement \(z_j\) will not lead to angular momentum. The same conditions may be used more generally for bigger displacements, and any bond lengths or angles. Also, this condition will yield the same plane irrespective of which particle is chosen as \(j=1\). Combining all these conditions, we can now determine the orientation of the mean plane for the position vectors \(_j\):
$$ \mathbf{R'} = \sum^{5}_{j=1}\mathbf{R}_j \sin(2\pi(j-1) / N) $$
$$ \mathbf{R''} = \sum^{5}_{j=1}\mathbf{R}_j \cos(2\pi(j-1) / N) $$
then the unit vector
$$ \mathbf{n} = \mathbf{R'} \times \mathbf{R''} / \left| \mathbf{R'} \times \mathbf{R''} \right|$$
is perpendicular to \(\mathbf{R'}\) and \(\mathbf{R''}\). Thus, we can use $\mathbf{n}$ to define the new \(z\)-axis. Finally, the \(y\)-axis, defined by unit vector \(\mathbf{m}\), can now be found by simply taking the crossproduct of $\mathbf{l}$ and $\mathbf{n}$. By converting coordinates to this new coordinate system, we can determine the ring’s puckering coordinates.
The ring puckering amplitude \(q\) and phase \(\phi\) for a ring of 5 particles are defined as:
$$ q \cos \phi = \sqrt{2/5} \sum z_j \cos 4 \pi j / 5 $$
$$ q \sin \phi = \sqrt{2/5} \sum z_j \sin 4 \pi j / 5 $$
We can simply calculate the puckering coordinates from the transformed coordinates for every snapshot.
4.4. Simulations
The structural distribution of colloidal cyclopentane is sampled with the computational model described in Ref.40) which is based on critical Casimir potentials 41) benchmarked onto experimentally measured chain length distributions and the bending rigidities of a dipatch particle system at various temperatures.
Here the computational model for tetrapatch particles interacting via critical Casimir interactions is presented at an off-critical binary mixture and the simulations of the conformational distribution of colloidal cyclopentane is discussed.
4.4.1. The Potential of the Tetrapatch Particle
The potential of the patchy particle system (Eq. [eq:ch3-V_tot]) has two contributions: the pair potential $V_{\text{pair}}$ (Eq. [eq:ch3-V_pair]) acting between the colloidal particles and a gravitational potential $V_{\text{gravity}}$. The total interaction is a summation over the pair potentials and the gravity over \(N\) particles.
$$ V = \sum_{i,j}^{N} V_{\text{pair}}(i,j) + \sum_{i}^{N}V_{\text{gravity}}(z_i) $$
$$ V_{\text{pair}}(i,j)= $$
$$ \infty \text{, if } D=r-\sigma\leq 0 $$
$$ V_{\text{rep}}(D_{ij}) + V_{\text{C}}(D_{ij}) S'(\Theta_i)S'(\Theta_j) \text{, if } D>0 $$
The pair potential is composed out of an isotropic repulsion \(V_\mathrm{rep}\) plus a critical Casimir attraction \(V_\mathrm{C}\) only effective at the patches via a switching function S’ of both particles \(i\) and \(j\). The repulsion and attraction are only a function of the radial surface-surface distance \(D_{ij}\) between two particles with diameter \(\sigma\) and centre-to-centre distance \(r\), while the switching function \(S'\) is dependent on the patch orientation with respect to the inter-particle vector.
In experiment, the tetrapatch particles and dipatch particles are synthesized from the same materials and assembled into various architectures in the same solvent: a water/lutidine (75/25%vol) binary liquid with 1.0 mM MgSO\(_4\). Only the physical dimensions of the dipatch and tetrapatch particles differ. Thus, one expects that the potential of the tetrapatch particles uses the benchmarked parameters of the dipatch system, i.e. surface charge $\Upsilon = -0.10$ e/nm\(^2\) and scaling wetting parameter \(w=0.47\), which are material properties.
However, significant bonding of the tetrapatch particles is only observed at temperatures of $\mathrm{d}T=T_{\mathrm{cx}}- T \leq 0.04$ where $T_\mathrm{cx}$ is the phase separation temperature. This indicates that upon increasing the temperature and approaching \(\mathrm{d}T = 0.04\) in experiment, the potential gets stronger and the critical temperature \(T_\mathrm{c}\) has not been crossed yet. This is in contrast to the theoretically predicted critical temperature at \(\mathrm{d}T=0.08\)42), and \(\beta=0.3265\) a universal scaling constant.)). The addition of salt to the solvent may affect the phase separation curve which leads to a shift of $T_{\mathrm{cx}}$.
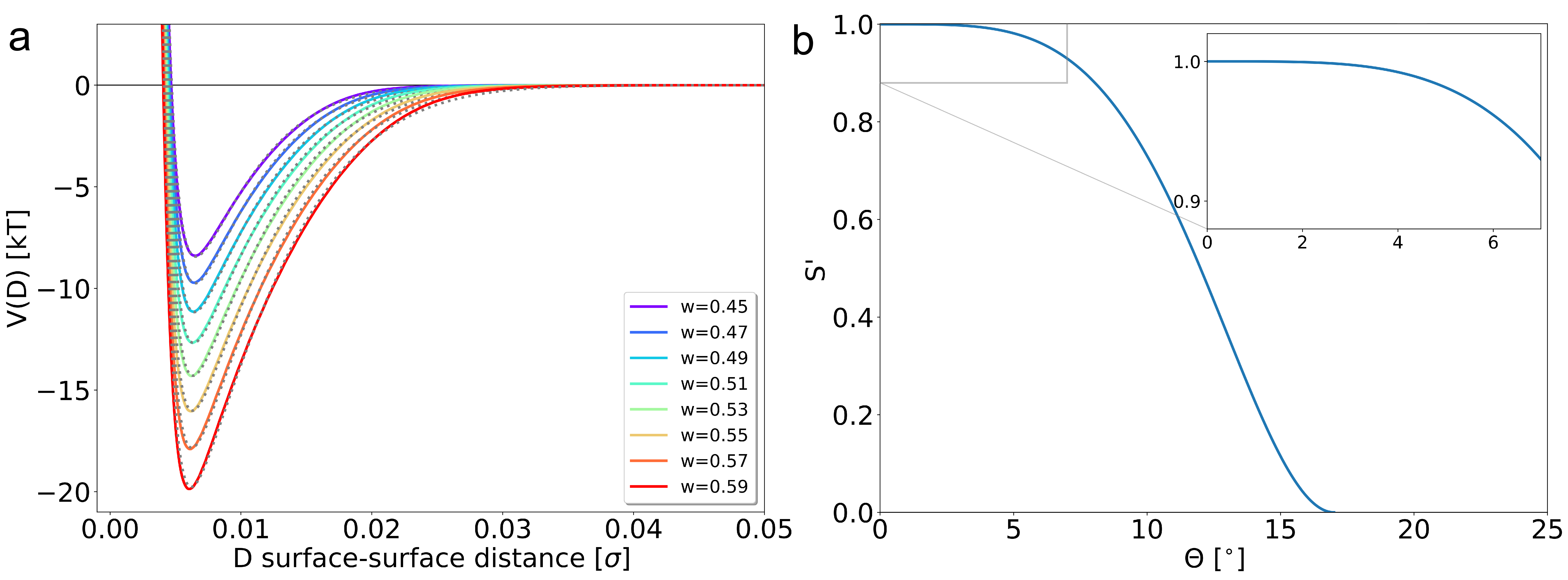
With the non-universal scaling constant \(B=0.765\) and wetting scaling parameter \(w=0.47\), patches of tetrapatch particles do not show significant binding at \(T=0.04\)43). Therefore, \(w\) is increased to ensure spontaneous formation of bonds. From an interaction strength with \(w \geq 0.55 \), there are colloidal cyclopentanes observed in an MC simulation at 15%area coverage including gravity. Figure 6a shows the pair potentials and their fit at various scaling wetting parameters \(w\) of a hydrophobic isotropic colloidal particle with $\Upsilon = -0.10$e/nm\(^2\), $R_\mathrm{p}= 0.5$ μm, and \(\Delta T=\) 0.04K immersed in the binary liquid.
The angular dependence of the interaction strength is captured by the switching function S which is a smoothly decaying function from 1 to 0 as shown in Figure 6b. As the patch geometry of the tetrapatch is similar to the particles from Ref44), we use the switching function
$$ S'(\Theta_i)= $$
$$ \frac{1}{2} \left[ 1-\cos \left( \frac{\pi(\cos\Theta_i -\cos\Theta_\mathrm{p})}{1-\cos\Theta_\mathrm{p}} \right) \right] \text{ , if } \cos\Theta_i\geq \cos\Theta_\mathrm{p} $$
$$ 0 \text{ , if } \cos\Theta_i<\cos\Theta_\mathrm{p}$$
is the angle between the patch vector $\mathbf{p}_{i}$ and the interparticle vector \(\mathbf{r}_{ij}\).
The gravitational potential is a function of the mass difference between the colloidal particle and the solvent. Tetrapatch particles are synthesized from four equal spheres of polystyrene (PS) surrounding one sphere of TPM with an ideal ratio $r_{\text{TPM}}$:$r_\text{PS} = (\sqrt 8-2)/2 $ which translates into a fractional volume \(\phi_{\text{PS}} = 1-\phi_{\text{TPM}} \approx 0.9825\).
4.4.2. Monte Carlo sampling of the Colloidal Cyclopentane Conformations
The computational system is composed of N=5 particles in a cyclopentane conformation. We sample the conformational distribution of the colloidal cyclopentane by performing 60000 cycles of 500000 single particle Monte Carlo steps. Bond breakage, if the critical Casimir interaction \(E_{\mathrm{C}}=0\), is not allowed as we are only interested in the conformational distribution of cyclopentane. Additionally, to mimic the experimental measurement accuracy, we add a Gaussian noise with zero mean and standard deviation of 0.1μm \(= 0.03 \sigma \) in the direction perpendicular to the wall.
4.4.3. The Conformational Distribution of the Colloidal Cyclopentane
Figure 7 shows the probability density of colloidal cyclopentane with the potential with \(w=0.55\) as function of puckering phase \(\phi\) and amplitude \(q_\mathrm{N}\) of system with and without gravity and the Gaussian noise. As observed in experiment, there is no preference for the envelope or twist conformation in any of the simulations. Thus, the puckering phase is not affected by the gravitational force acting on the colloidal particles and the measurement inaccuracy in the z-direction.
The puckering amplitude does depend on the presence of gravity and the measurement inaccuracy in the \(z\)-direction. Without gravity the maximum of the probability density \(q_{\mathrm{N,max}}\) is shifted toward larger \(q_\mathrm{N}\) values of approx. \(0.15\) compared to the experimental measurement. This means that the colloidal cyclopentane is more bend in a system without gravity. With gravity the colloidal cyclopentane is flattened and the maximum of the probability density is close to experiment \(q_\mathrm{N}=0.06\). The effect of the Gaussian noise is making the colloidal cyclopentane appear more bend than it actually does. This effect is mainly observed in the system without gravity. An increase of density at \(q_\mathrm{N}\) values larger that \(q_{\mathrm{N,max}}\) is observed which shift the complete curve.
4.5. Patchy Particle Assembly
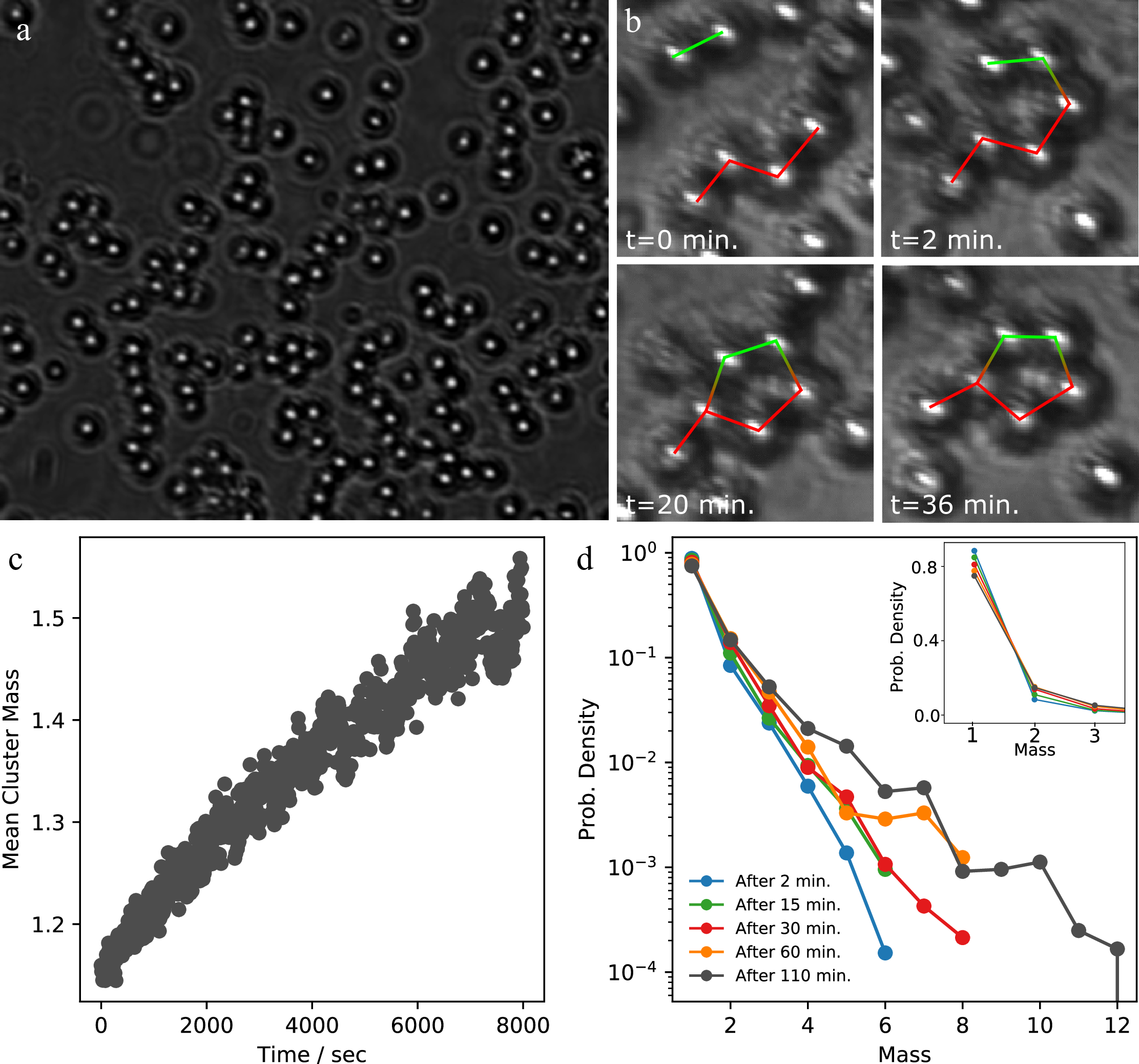
We typically leave the particles to assemble at constant temperature for several hours. In Figure 8, we show the typical process of assembly in a sample with a mix of di- and tetra-patch particles, here at \(\Delta T=\) 0.05°C and number density \(\rho= \) 0.015 μm\(^{-2}\). A bright-field microscope image of the assembled structures after 2 hours of assembly is shown in Figure 8a. A zoo of colloidal molecules is observed, from butanes and propanes to longer, polymer-like chains.
In Figure 8b we show a few snapshots revealing the assembly of colloidal methyl-cyclopentane. This process begins with butane and propane, which react to form hexane. This longer chain is now in a conformation in which it can easily form methyl-cyclopentane by reacting its first atom with the fifth atom in the chain. The molecule can also change to a conformation that reacts to cyclohexane by flipping atom 6 from the eclipsed to the staggered position. However, due to the quasi-2D nature of our system there is an energy penalty associated with this conformational change, making the formation of methyl-cyclopentane more likely.
Figure 8c and d show the growth of the mean cluster size and cluster size distributions. Initially, at the start of the measurement (\(\Delta T = 0.26°C\)), there is no clustering. As soon as we increase the temperature to \(T=0.05°C\), particles start assembling, and clusters start to grow. Figure 8c shows the growing average cluster size as a function of time. After 2 hours, when the measurement is stopped, an equilibrium cluster size has not been reached yet. The cluster mass distribution at different times is shown in Figure 8d. After 2 minutes several structures have already formed. As time continues, the slope of the distribution becomes less steep, indicating large structures start forming, although singlets are still the major component. This behaviour is qualitatively in line with what we expect for a growing network according to Wertheim theory 45), and will be discussed in depth in chapter 6. Also, it appears that at later times, structures with certain number \(n\) of particles are clearly preferred, such as \(n=\) 5, 7, and 10. We note that here, however, cyclic and linear structures are both counted; for a distinction of cyclic structures alone, see Figure 2.
4.6. Conformations of Different Colloidal Molecules
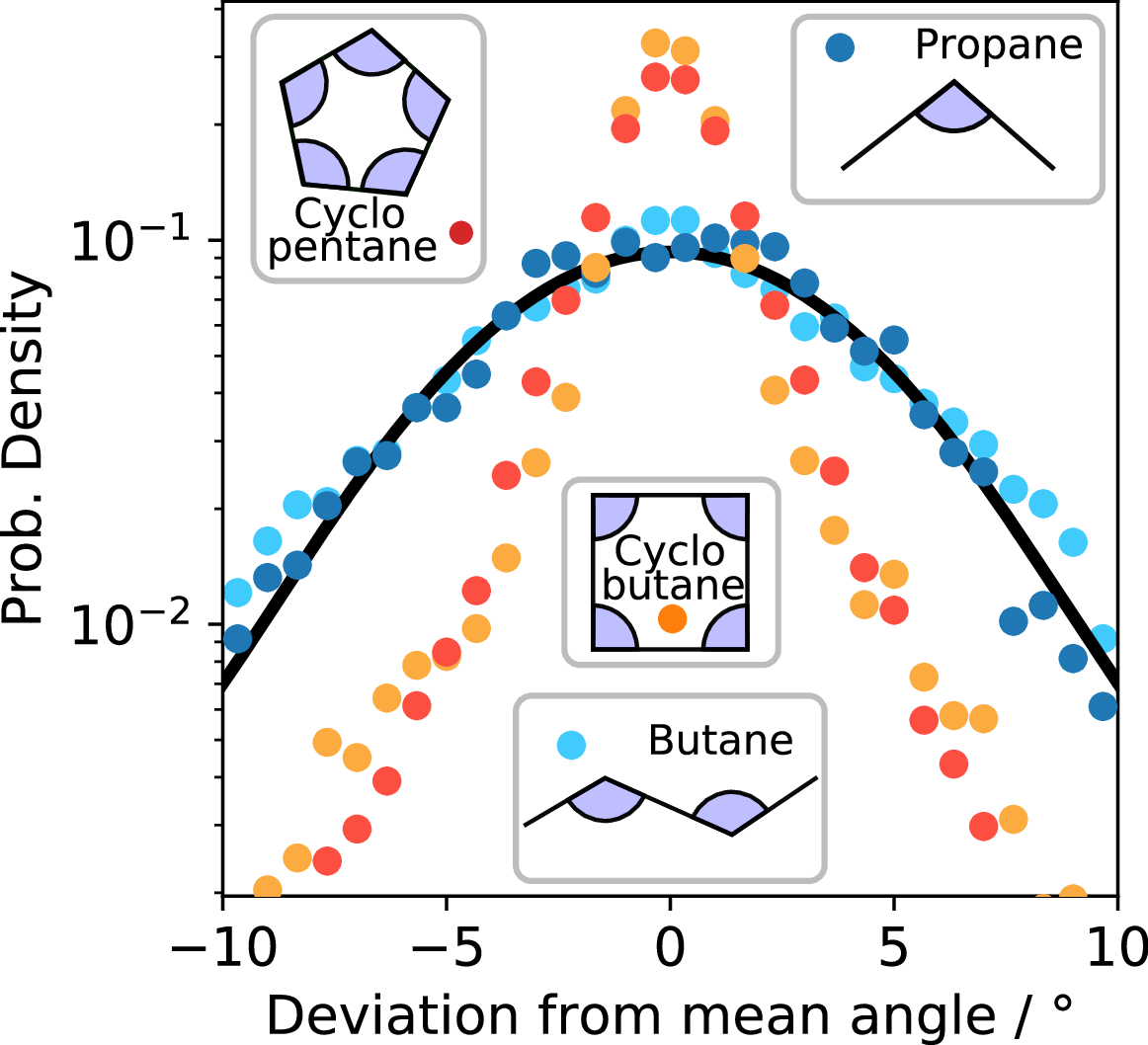
Apart from cyclopentane, which is treated quite thoroughly in the main text, we observe many other structures. To better understand the puckering of cyclic molecules, we investigated the bond angle distributions of a range of structures, from linear to cyclic compounds, as shown in Figure 9. We imaged propane, butane, cyclobutane and cyclopentane using bright-field microscopy in the same sample at constant temperature (\(\Delta T=0.05°C\)), and measured their 2D-projected bond angles. From repeated fast imaging, we then determined bond angle distributions for all structures, as shown in the figure. We note that this projected 2D angle differs from the 3D angles explored in the main text, but does allow us to obtain significant statistics to compare the different linear and cyclic structures in terms of their bond stiffness.
Interestingly, propane and butane, both linear structures, one with three, one with four particles, show very similar angle distributions. Both species are free to move around their preferred angle: there is no steric hindrance or confinement effect from being in a ring. In fact, by treating the particle bond as a simple spring, we can determine a spring constant from the probability distributions in Figure 1. The unconstrained spring constant of propane and cyclobutane is \(k_{\mathrm{bend}}= 3.4 k_\mathrm{B}T\)rad\(^{-2}\), shown as the solid black line. In contrast, the cyclic molecules (cyclobutane and cyclopentane) show much narrower angle distributions, which we associate with the constraint of the cyclic structure. The resulting ‘spring constant’ of the cyclic structures is thus much stiffer than the one of the free bond angles of the linear structures.
4.7. Timescales

To probe the typical timescale of the ring transitioning between conformations, we acquired bright-field images of rings at a frame rate of 2 \(s^{-1}\). In each frame, we track the particles in a horizontal plane and determine the angles \(\) between the projected particle positions. We take these time-dependent angles to calculate the time autocorrelation:
$$ g_\mathrm{2}(\Delta t) = \frac{\left\langle \theta_i(t) \times \theta_i(t+\Delta t)\right\rangle_{i,t} }{\left\langle \theta_i(t)^2\right\rangle_{i,t} }, $$
where we average over all five angles and the observation time interval \(\Delta t = 0.5\) seconds. We plot a typical example of the autocorrelation of the angles over time in Figure 1. Generally, we find there is a fast component, \(\tau_1\), of around 9 seconds, and a slower component, \(\tau_2\), of around 25 seconds. We associate \(\tau_1\) with the diffusion of the particles, as this is approximately the expected timescale for a 3.7 μm particle to diffuse its own radius. Furthermore, we associate \(\tau_2\) with the configurational changes, i.e. pseudo-rotation of the ring, which is further confirmed by the anticorrelated motion of neighbouring particles, indicating the characteristic change between conformations while keeping the overall puckered state (see Figure 3e).
4.8. The Bending Energy of Cyclopentane
In this chapter, we have combined our experimental observations of the puckering ring with simulations for the entropic component to extract the pure bending energy of the ring as a function of \(q_\mathrm{N}\). To do this, we start with the free energy as a function of puckering amplitude \(q\), given by
$$ F(q) = U(q) - TS(q) $$
where \(U\) is the Boltzmann averaged energy caused by bending, \(T\) the temperature, and \(S\) the entropy. Assuming this free energy to exhibit a Boltzmann distribution in thermal equilibrium, the probability of observing a configuration with puckering amplitude \(q\) is given by
$$ f(q) \sim e^{-F/k_\mathrm{B}T} = e^{-U/k_\mathrm{B}T} \cdot e^{TS/k_\mathrm{B}T}. $$
Rewriting this gives:
$$ ln(f(q)) = -U(q)/k_\mathrm{B}T + S(q)/k_\mathrm{B} + C $$
$$ U(q)/k_\mathrm{B}T = -ln(f(q)) + S(q)/k_\mathrm{B} + C, $$
with \(C\) a constant. The entropic contribution is given by the multiplicity \(\Omega\) as determined from the simulations of random independent displacements, so:
$$ S(q) = k_B \cdot ln(\Omega(q)) $$
$$ U(q)/k_BT = ln(\Omega(q)) - ln(f(q)) + C $$
$$ = ln(\Omega(q) / f(q)) + C $$
$$ = ln(P_{0} \cdot P(q) / f(q)) + C $$
$$ = ln(P(q)/f(q)) + C', $$
with \(\Omega\) the number of microstates, and \(P(q)\) the entropic simulation observation frequency.