Table of Contents
Introduction
1)Defining colloids in the traditional way is a bit like defining puppies as young dogs; though technically accurate, it doesn’t quite capture their appeal.
1. Emergence
A common definition of a molecule is the following2):
The smallest particle of a substance that retains all the properties of the substance and is composed of one or more atoms.
However, the physical properties of a material are almost always different from the physical properties of a single molecule - if we can even speak of physical properties in this context. The difference in properties between a material and its constituent molecules is an example of what we call emergence: an entity has properties different from (the sum of) its parts, the properties emerge only when parts interact in a larger collection. In this case: an assembly of molecules, like a crystal, shows behaviour that a single molecule does not directly hint at.
Emergence is not just an abstract idea, we can recognize the principle in action in our daily lives. Chess is a simple game which can be explained to an 8-year-old, yet its simple rules lead to a complex strategic game that has remained interesting for the past \(1500\) years. The intricate patterns formed by wind on a sand-dune are hard to predict if one only knows about sand and wind. Life in particular is full of emergent properties. The archetypical example of emergence is consciousness: it still puzzles us how electrochemical potentials along cell membranes can lead to sentience. There are many more examples of emergence in biology, and in the context of this thesis, proteins make for an excellent example.
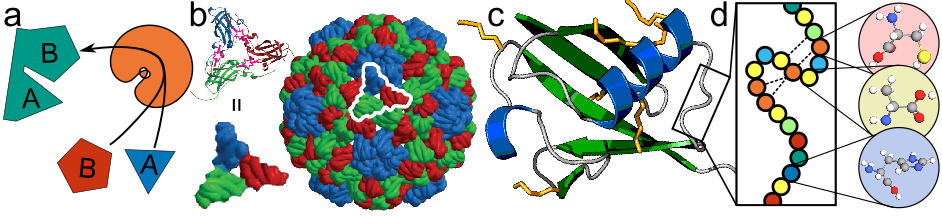
Proteins have many biological functions, ranging from ‘simple’ catalytic activity (Figure 1a) to sophisticated tasks like causing muscles contractions or assembling large superstructures, like viruses (Figure 1b). Each protein has a unique complex structure: a protein is a long chain molecule that twists and folds in very specific ways, see for example Figure 1c. The chemical groups these folds expose are responsible for the behaviour of the protein; it may attract other proteins to form specific assemblies, such as in Figure 1b, or it may stabilize certain reaction intermediates, catalysing reactions (Figure 1a). When we zoom in, however, we see that all proteins are chemically very similar: a protein chain always consists of just twenty different building blocks (amino acids) combined and repeated in different ways, Figure 1d. The order of these amino acids determines the folding of the protein, and in turn its properties. Even with a near-complete understanding of these building blocks, predicting the function of a protein based on its amino-acid sequence is extremely challenging. The complex interplay between building blocks is very hard to predict; a small change could make no difference, but could also have extremely far-reaching effects: for example, changing a single glutamic acid to a valine in the protein hemoglobin causes it to assemble in the wrong way, leading to sickle-cell disease 3).
Science is often reductionist, meaning that we try to explain a system by understanding its components. The well-known ‘theory of everything’ is the exponent of this view: intuitively, if we understand all the exact fundamental laws governing the smallest particles, we should understand everything that consist of them; everything. Unfortunately, in real life such a reductionist view will reveal almost nothing about the behaviour of everyday objects; in practice it is simply not very likely that we can ever use the theory to understand life and its chemical intricacies, let alone mundane phenomena such as bird flocking. The emergence of unexpected phenomena from well-understood building blocks is responsible for this disconnect, and its study is therefore necessary if we want to understand the world around us.
2. Organization
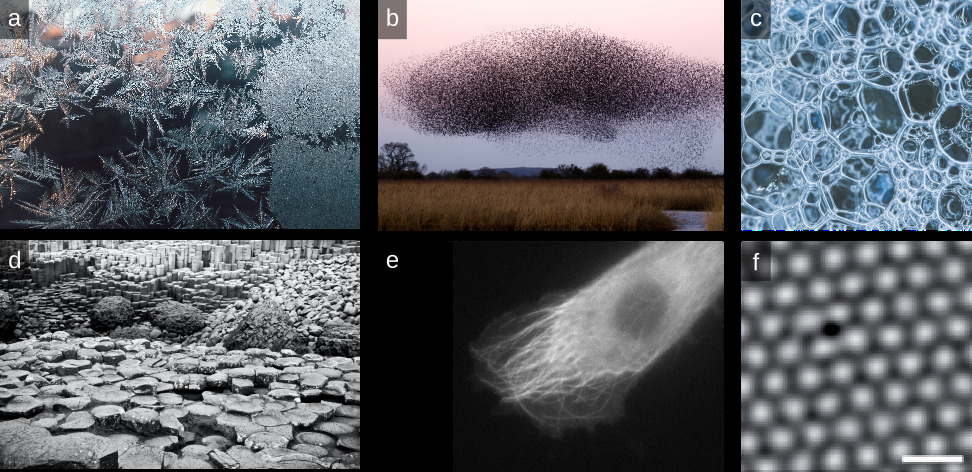
A typical emergent process is self-organization, the formation of patterns and structure, without an external template or guiding force, see Figure 2. This universal tendency to self-organize is encountered in all domains of science, from astronomy - where stars cluster into galaxies - to ecology - where individuals form ecosystems. It is therefore of fundamental interest to understand what common principles underlie these phenomena. Furthermore, self-organization has the tendency to manifest in similar ways across seemingly unrelated systems: the shape of basalt columns in Figure 2d for example is extremely common in nature - hexagons are found in materials ranging from soap bubbles (Figure 2c) to graphene (Figure 2f).
A useful distinction can be made between self-organization, in which a system organizes under an energy input, and self-assembly, in which a system organizes in equilibrium: bird flocking (Figure 2b) is self-organization, while the formation of ice crystals (Figure 2a) is self-assembly. In this thesis, we deal with self-assembly. Self-assembly always has three basic ingredients: (i) building blocks, (ii) an interaction between those blocks, and (iii) a source of movement which can bring the blocks together and makes them organize. In a self-assembled system, the interaction between building blocks is always local, meaning that there is no awareness of the larger structure; a building block is simply following its local interactions. The three ingredients can easily be identified in our examples: the protein in Figure 1c (i) consist of amino acids, which (ii) interact via inter- and intramolecular forces and (iii) move around via Brownian motion, the random jiggling of molecules.
3. Colloidal Particles

An intuitive, simple system for studying self-assembly and emergent properties are colloidal particles. Colloidal particles are small particles with a size between roughly \(1\)nm and \(1\)μm, suspended in a solvent, moving by Brownian motion4). )). Examples of colloids in our day-to-day live include foodstuff (whipped cream, mayonnaise), soap, some gems (pearls, opals), and ink (including e-ink displays) among many other things (see Figure 3a-d).
Using colloidal particles as building blocks in self-assembly is compelling, because they are simple and easy to control: colloidal particles are typically spherical uniform blobs (see Figure 3e-g), without complex internal workings as opposed to molecules. On top of that, colloids can interact with each other via a myriad of different driving forces over which we can exert good control. Finally, colloids are small enough that thermal motion provides movement ‘for free’ due to the constant random wiggling of molecules.
Even the simplest colloidal particles can self-assemble into a fascinating range of structures. Depending on the system conditions, particles can assemble into highly ordered structures, like hexagonal crystals (Figure 3h), or into disordered assemblies like gels and glasses (Figure 3i). By making precise changes to the building blocks and their interactions, like adjusting attractive strength or size dispersity, we can influence the assembly of colloids. Furthermore, colloids are relatively straightforward to investigate experimentally due to their simple preparation and easy-to-vary properties like charge. On top of that, their size is convenient: colloidal particles are large enough to be visible under a regular optical microscope, and assemblies can easily be characterized by light scattering experiments.
Interestingly, many of the phases colloidal particles assemble into are reminiscent of atomic states of matter (gas, liquid, solid crystals, etc.) 5). This may not be so surprising when we consider that the 3 components of self-assembly are actually quite similar in atomic and colloidal phases. Atoms, for all their complexity, often behave as simple uniform spheres, just like simple colloidal particles. Interactions between atoms and colloidal particles have different origins, but are of similar relative range and strength, and both atoms and colloids jiggle around due to thermal motion. This has earned colloidal particles the name of big atoms 6). Although atoms are of course very different from colloidal particles, their collective properties are surprisingly similar. This is not a recent realization; the similarity in behaviour of atoms and colloids led to the experimental conformation of molecules in the first place in 1909 7).
3.1. Anisotropy

Although colloidal assembly of spherical particles is already intriguing, one cannot help but wonder: what happens in more complex systems? What kind of structures can be created if we deviate from uniform spheres? Apart from simple human curiosity, these questions have scientific relevance as well: modified building blocks can lead to new emergent material properties. Understanding the interplay between building block and the material they assemble into has intriguing prospects: one of the paradigms of soft matter is that the microstructure of a material controls its macroscopic properties. With absolute control over material microstructure, we could engineer interesting material properties that are hard to obtain in conventional bulk materials. Examples of such traits range from mechanical properties, such as a negative Poisson’s ratio 8) and other properties sought after in the field of metamaterials 9), to opto-electronic properties, like a photonic band-gap 10).
What do we mean by more complexity? The most obvious change one can make to a particle is to go beyond a simple spherical shape: the behaviour of a perfectly symmetrical spherical particle is generally well understood, so studying the effect of different shapes is a natural step to take 11)12). For instance, cubic colloids (maybe unsurprisingly) tend to assemble into cubic crystals, as shown in Figure 4a, but can also assemble into a range of slightly shifted lattices, depending on the assembly conditions 13)14). Rod-like colloids display a rich phase behaviour not seen in spherical particles. Aside from the usual liquid and crystalline phases, liquid crystal phases such as the nematic phase, in which particles have no positional order but are all rotated in the same direction 15), and the smectic phase, in which rods form aligned layers (shown in Figure 4b) 16), are observed. These phases are highly relevant to technological applications, and are found in liquid-crystal displays (LCDs). More exotic particle shapes, like the magnetic dumbbells in Figure 4c, can assemble into complex structures which are not always easy to intuitively predict. At low density, the particles assemble into one-dimensional chains, which start interlocking if the density is increased, leading to a lattice consisting of ordered chains 17).
Another, more controlled way of introducing complexity to a colloidal system is to make use of inhomogeneous particles; instead of a single component, a particle is composed of two or more different materials. The most basic example of this is the so-called Janus particle, named after the two-faced Roman god of duality. Two halves of the particle consist of a different material, which react differently to the environment and/or other particles, see Figure 6a, where half the particle is orange, and the other half is grey. With the improvement of synthetic methods in the past decade, even more sophisticated particles can be engineered, so-called patchy particles. Patchy particles have a surface with well-defined patches of a different material, see Figure 6b. The patches are typically designed to attract each other, and their placement is chosen such that a particle has limited valency and directional bonding, meaning that we control exactly where particles will attach and assemble. Essentially, patchy particles are microscopic lego-bricks: by controlling how two particles fit together, we aim to control the superstructure they assemble into, and thus engineer material properties.
3.2. Patchy Particle Assembly
Simulations and experiments of patchy particles have yielded a huge variety of interesting self-assembled structures and phases. Colloidal assemblies typically fall into one of two categories: periodic superstructures or finite assemblies. In this section I will highlight the importance of each category, and give a short overview of published work on these structures.
3.2.1. Periodic Superstructures
Large colloidal superstructures consist of many particles, typically, but not necessarily, with a certain repeating motif or long-range order. Non-patchy colloidal particles have been assembled into large superstructures for decades, initially mainly as a model system for atomic phases 18)19)20). As the field matured, assemblies came to be regarded as more than just a model system: they are self-assembling materials with their own interesting mechanical 21)22), electronic 23)24) and optical 25) emergent properties.
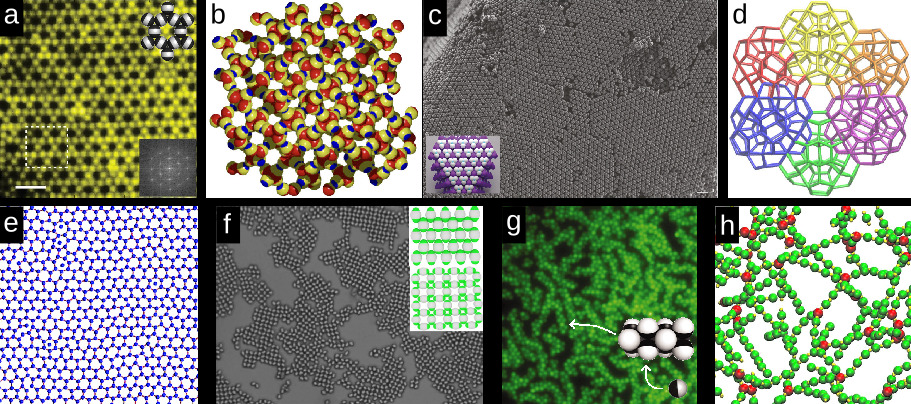
When the idea first developed to use patchy particles to further explore the engineering of colloidal materials, their preparation in the lab was not experimentally feasible 26)27). However, patchy particles are relatively easy to model in silico, so experimental limitations did not stop theorists from producing many models and simulations for a range of patchy particle models. Early examples of such predictions include the diamond lattice 28) and empty liquids 29). It took years before improvements in synthetic production of patchy particles lead to the first example of an assembled patchy particle periodic superstructure: the kagome lattice. The kagome lattice, shown in Figure 5a, consists of dipatch particles, where each patch binds two other patches, leading to the formation of a star-like pattern 30). Although this structure is not of any particular practical use, it did demonstrate that patchy particles can be used for experimental assembly of large non-trivial superstructures; it was the first step on the path to controlled microscopic engineering of large superstructures using patchy particles.
Despite this success in generating a patchy-particle superstructure over a decade ago, other experimental examples remain rare; the reliable assembly into large superstructures remains very challenging. An illustrative example is the diamond lattice, formed by tetrahedral particles ordered into repeating 6-membered rings, see Figure 5b&c. Colloidal diamond is one of the earlier predictions for a possible phase built from tetrahedral particles31) 32). The lattice is of particular interest because it has a photonic band gap, which allows precise manipulation of light 33)34). Unfortunately, reaching this state experimentally remained impossible for a long time, mainly due to two problems: spherical tetrapatch particles have no intrinsic preference for staggered or eclipsed bonding conformation 35), and the formation of 5-membered rings is kinetically preferred and stabilized 36). These 5-membered rings can then form energetically stable buckyball-like clathrates, see Figure 5d. Recently, these challenges have finally been overcome experimentally, 15 years after its theoretical description, by combining a geometrically controlled bonding valency with a specific shape, as shown in Figure 5c 37).
The field remains in a state where experimental results are highly sought after. Simulation results are often hard to confirm experimentally because they underestimate or ignore the importance of kinetic pathways toward predicted structures, or use particle designs that are experimentally not feasible. Although this is a known issue, and significant effort is expanded to take it into account, it remains challenging to translate results from simulations to experiment 38)39)40). Despite these difficulties, simulations and the few experimental examples that currently exist in literature give us a glimpse of the microscopic architecture that surely will become more prevalent in the future of designing smart materials.
Two more examples of highly ordered periodic superstructures shall be briefly addressed here to highlight the rich morphological variation patchy particle structures can display. Figure 5e shows a honeycomb lattice, formed by trivalent particles confined to a plane, similar to how graphene is formed by trivalent carbon atoms. Colloidal graphene is expected to display some interesting properties which graphene also exhibits: a photonic and phononic bandgap 15,45–47, and topologically protected states. Another example is shown in Figure 5f, where dipatch particles form two structurally distinct square phases. By changing the patch-to-bulk size ratio, the system can be tuned to assemble into a wide variety of different periodic structures 41). This rich variation in structural morphology from simple di- and trivalent particles highlights once more the potential for complex microscopic architecture resulting from assembly of patchy particles.
Not all large superstructures are ordered or crystalline; some are fundamentally unordered, even in equilibrium. For instance, simple janus particles can be assembled into highly structured worms, Figure 5g. These worms themselves however, do not have a clear order with regard to each other, and assemble into a gel-like structure. An even more exciting example is the hub-and-spoke network we obtain by mixing di- and tetravalent particles. Simulations show the formation of central hubs of tetravalent particles connecting chains of divalent particles; a snapshot of such a network is shown in Figure 5h. A network formed by patchy particles is predicted to be a so-called equilibrium gel 42)43), a state which is of fundamental interest to our understanding of gelling, a ubiquitous process in the natural world.
3.2.2. Finite Assemblies

Besides the more traditional large superstructures, there has been an increased interest in smaller finite-sized assemblies of colloids in the past decade. Colloidal clusters of isotropic particles are interesting because their limited size makes the self-assembly easier to study and understand quantitatively 44)45). Furthermore, these clusters can display exotic optical properties 46)47).
Small clusters of patchy particles are well studied compared to large superstructures, because smaller assemblies are simply easier to control and understand. As we discussed, the assembly of patchy particles is not a trivial matter, so achieving directed self-assembly in small cluster is reason enough to celebrate 48)49). That is not to say that these clusters are not useful: as isotropic particles can serve as a model for atoms, small colloidal assemblies can serve as a model for a molecule, and the study of so-called colloidal molecules has become a fashionable use of these clusters 50). In a colloidal molecule, colloids act as big atoms, mimicking the bonding arrangements of their atomic counterparts, see Figure 6c&d for examples. Because colloids can be directly observed, their behaviour is much easier to study than those of atoms. For instance, studies into the reaction kinetics of colloidal molecules show interesting similarities with ‘regular’ atomic reactions 51). Colloidal polymers, consisting of identical repeating particles (examples shown in Figure 6e&f), are another clear example. The growth and dynamics of such chains is surprisingly similar to that of atomic polymers 52)53).
Finally, a strong motivation for the study of finite-sized particle assemblies is that these clusters are often the basic motifs of any larger superstructures that these particles could assemble into 54). Much like molecules are studied because they are the smallest unit of the materials around us, it is appealing to study small colloidal assemblies as the building block for larger superstructures. An example is the structure shown in Figure 5f: the dipatch particles form colloidal polymers with specific geometries that are also found in the larger assembled superstructure 55).
4. Thesis Outlook
This thesis aims to experimentally address the self-assembly of patchy colloids. Although I treat a few specific cases of colloidal assembly here, this work should be seen in the larger context of understanding and controlling microscopic assembly.
Chapter 2 deals with the experimental methods and core concepts that are used in this thesis. I briefly discuss the properties and synthesis of the colloidal particles used in this thesis. I then quickly give a practical guide to the critical Casimir force, the driving force for colloidal assembly. Finally, I describe how we proceed from sample preparation to experiments and conclusions, and which techniques and analysis steps this involves.
In Chapter 3, we dive into the physics of small patchy particle assemblies in seriousness, looking at a small colloidal ring made up of five tetrahedral patchy particles. I discuss how these colloidal cyclopentane rings can undergo the same chemical transformations as their atomic counterparts. Transitions between chair and twist conformations in colloidal cyclopentane are observed directly, and we elucidate the interplay of bond bending strain and entropy in the molecular transition states and ring-opening reactions.
Chapter 4 explores colloidal graphene, the analogue of atomic graphene assembled using pseudo-trivalent patchy particles confined to a plane. Direct observation of the formation and healing of common defects, like grain boundaries and vacancies, grants us insight into what may occur during the growth process of atomic graphene, normally hidden due to the extreme conditions in which it takes place. These direct observations reveal that the origins of the most common defects lie in the early stages of graphene assembly, where pentagons are kinetically favoured over the equilibrium hexagons of the honeycomb lattice, subsequently stabilized during further growth.
In Chapter 5, we dive deeper into the system of pseudo-trivalent patchy particles confined to a plane and map the full phase diagram of the system. Apart from the colloidal graphene described in Chapter 4, we observe regions in the phase diagram where a triangular lattice and amorphous network are formed. We investigate these unexpected condensed phases, revealing their shared structural motifs. Combining results from model and experiment, we elucidate the energetics of the three condensed phases and construct the phase diagram of the system. This chapter illustrates the rich phase behaviour a relatively simple patchy particle system can display.
Finally, Chapter 6 treats an unordered patchy particle superstructure: networks constructed from a mixture of di- and pseudo-trivalent patchy particles. This network is a so-called equilibrium gel, and has some very counterintuitive properties: while the properties of a ‘regular’ colloidal gel strongly depend on the conditions of its formation, the history of an equilibrium network does not influence its eventual properties. On top of that, we can use a corrected Flory-Stockmayer theory to accurately describe and predict the behaviour of the system as a function of the normalized number of bonds.